Leanote, Not Just A Notepad!
Knowledge, Blog, Sharing, Cooperation... all in Leanote
About Leanote
Knowledge, Blog, Sharing, Cooperation... all in Leanote
About Leanote
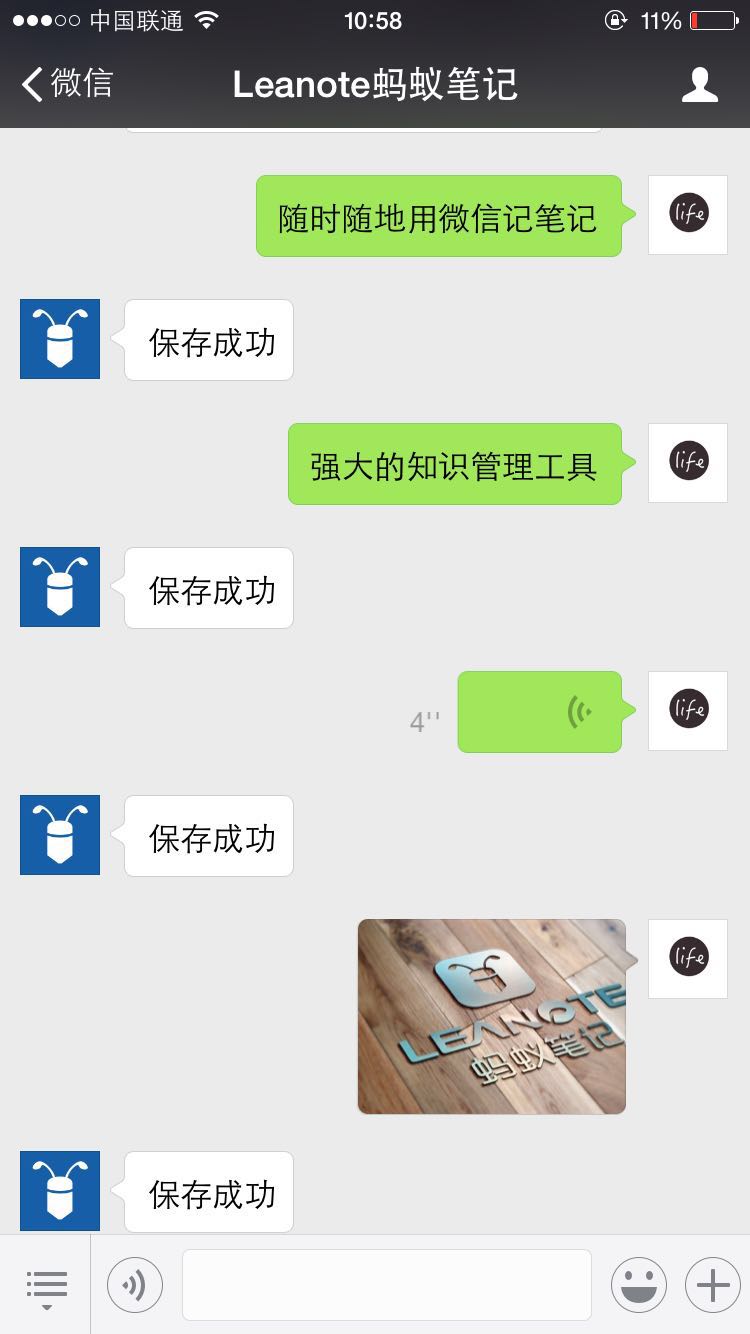
 微信扫一扫关注"Leanote蚂蚁笔记"公众号
微信扫一扫关注"Leanote蚂蚁笔记"公众号

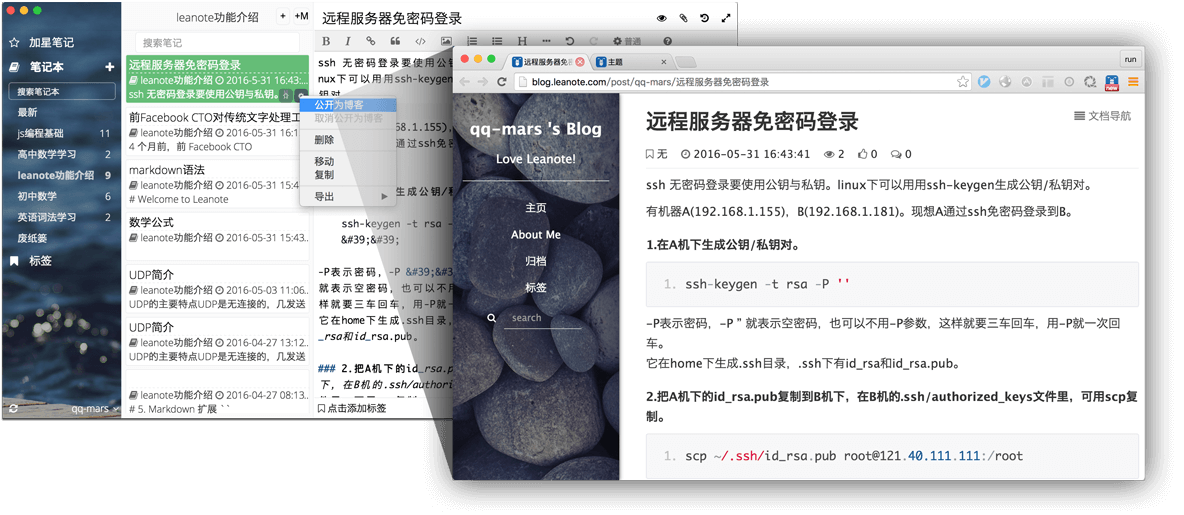
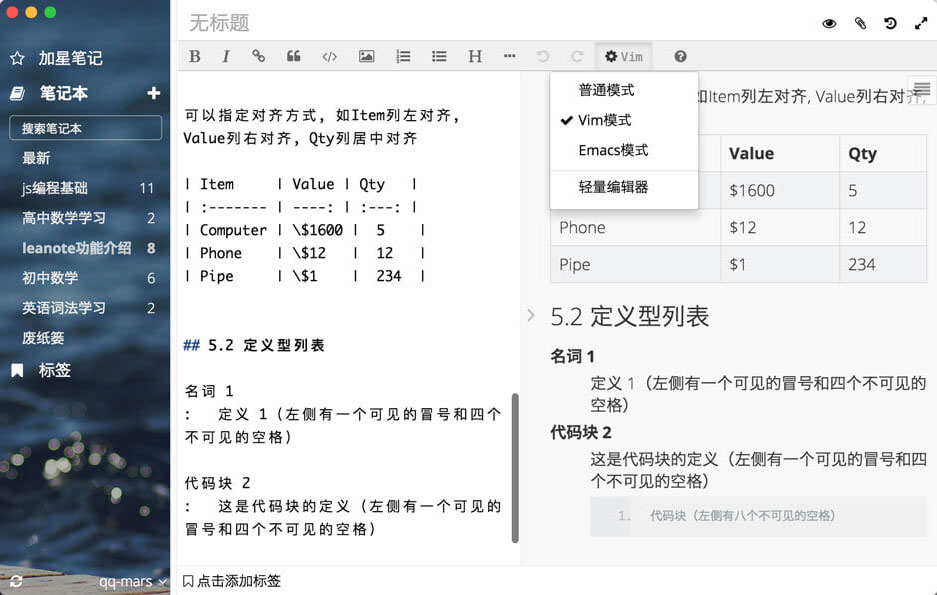
涵盖所有主流语言的代码高亮,随心所欲在Leanote里写代码,记知识。
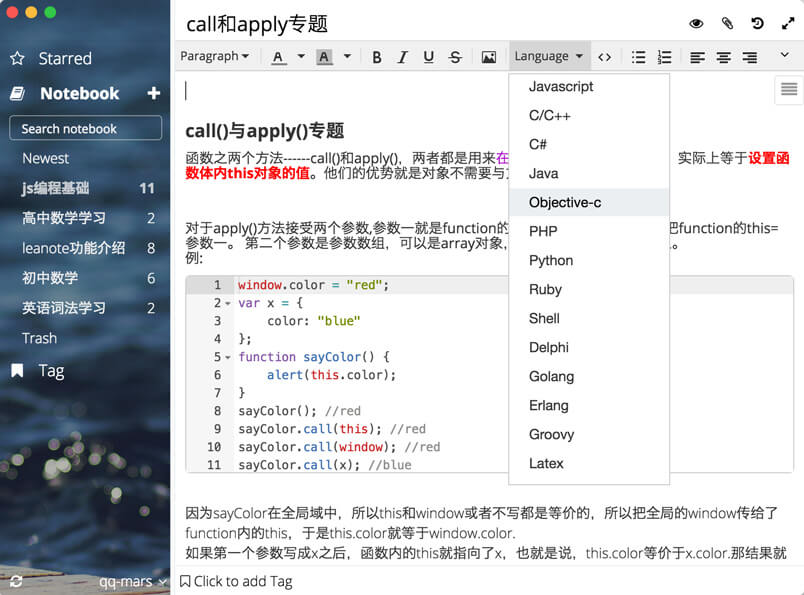
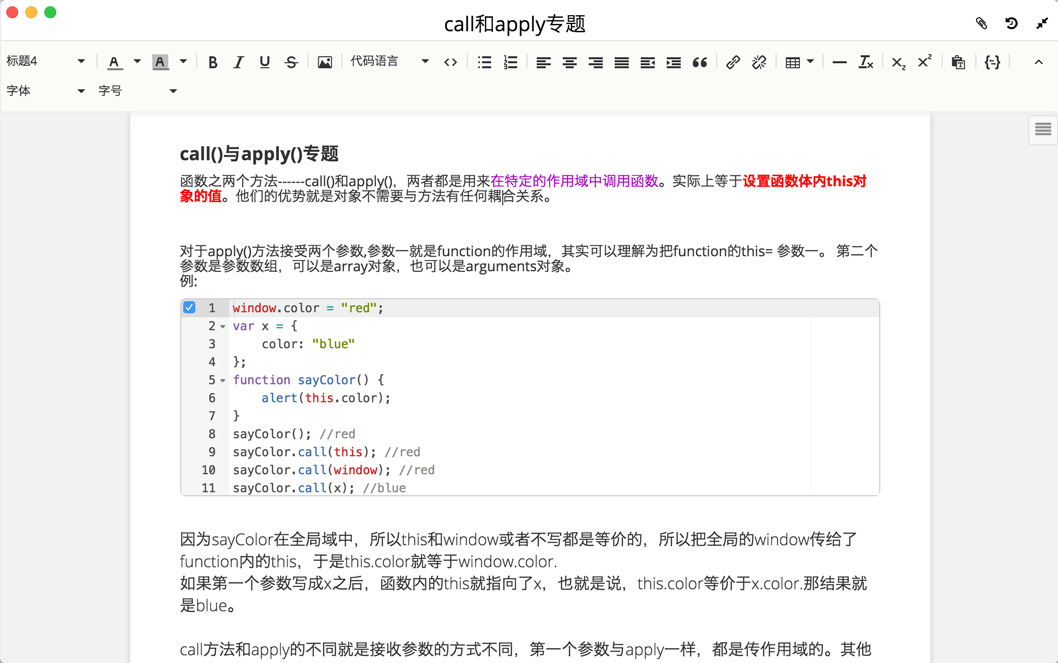
实时同步预览,你只需使用键盘专注于书写文本内容,就可以生成印刷级的排版格式。
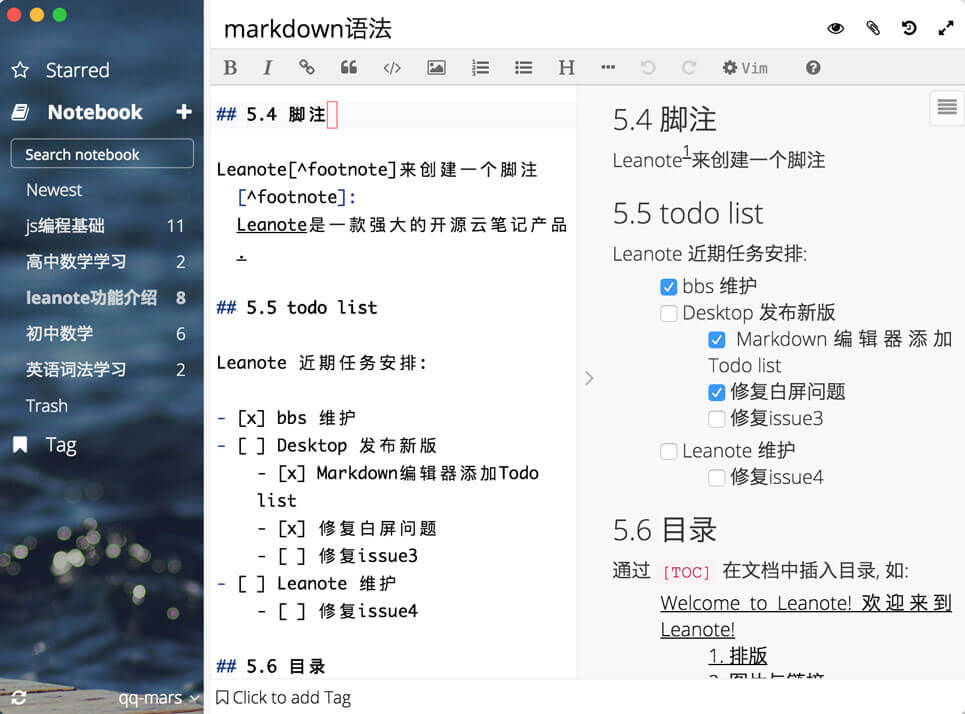

极客的最爱,让双手不离键盘,轻松提升笔记效率。